Charged black holes
Written 30th of July 2023 Last updated 30th of July 2023 Abstract
Here we will give a short overview of
this
paper, where we considered the inspiral of two black holes
that carry electric charge, either from electromagnetism,
or some dark sector \(U(1)\) charge. Usually, all astrophysical
black holes are assumed to be electrically neutral, see for
example
this
review. The argument for this is very strong, since the timescale
for neutralisation would be very small for significantly
charged black holes due to among other Schwinger pair-production,
or accretion of oppositely charged matter from the environment.
However, there are ways to avoid short neutralisation timescales
for astrophysical black holes, for example by use of mini-charged
dark matter. See
this
paper. The following work is covered in detail in my
thesis.
The field of gravitational waves is moving rapidly, and
so it should be kept in mind that a lot of work has been
done since the time of this project, and the detector
network has grown and increased its sensitvity. Idea
The use of matched filtering statistics in the
detection- and parameter estimation pipelines of
LIGO/Virgo has the consequence that the detectors will
have high sensitivity only to signals that are already
properly modelled, such as circularly inspiraling black
holes with different masses and spins. Black holes will
in principle come with one extra parameter, which is the
electric charge they carry. Since this is usually
neglected because of astrophysical decharging
mechanisms, if there somehow where a binary carrying
electric charge merging, we might either miss the signal
entirely, or interpret it wrongly in terms of our
uncharged templates during parameter estimation. In this
work, we set out to explore at lowest order what size of
error such a projection effect can have on the mass
estimation of the binary, and also how large signal
losses we might get. Below we illustrate how the noise
and signal blends together in a time-series from the
detector. The signal amplitude has for presentation been
exagerrated, and the y-axis is normalised to unity. The
time is in units of seconds. 
Orbit
The first step towards finding the emission of
gravitational waves in the slow inspiral regime of the
merger, is to find the quasi-static orbit. We are here
assuming that the orbital parameters are changing slow
with comparison to the timescale of the orbit, so that
the orbit at any moment is well described by constants
of motion such as orbital energy and angular momentum.
After finding the orbit, we will calculate the expected
emission for a particle that follows it, and then couple
those emissions to the expressions for orbital energy
and energy momentum to solve for the orbital parameters
as a function of time. Since the Coulomb potential which is set up by charges
we introduce goes like \(1/r\) like the gravitational
potential, we can add them together by use of an
effective gravitational constant like
$$
\Phi = - \frac{\tilde G M \mu}{r^2},\quad
\tilde G = G_N \left(
1 - \sigma_1 \sigma_2
\right),
$$ where \(\sigma_i = q_i/m_i\) is the black hole's charge
to mass ratio, \(m_i\) is its mass, and \(M=m_1+m_2\)
and \(\mu=m_1 m_2/m\) are the total mass and reduced
mass respectively. From here, for the quasi-static
orbit, everything is as with the gravitational case,
traded in this gravitational constant, and so we can
find the Keplerian orbit
$$
\begin{eqnarray}
r &=& \frac{a(1-e^2)}{1+e\cos\psi},\\
a &=& \frac{\mu M}{2 |E|},\quad e = \sqrt{1 + \frac{2 E L^2}{M^2\mu^3}},
\end{eqnarray}
$$ where \(a\) is the semi-major axis and \(e\) is the
eccentricity, while \(E,L\) are the orbital energy and
angular momentum respectively. We can find the lowest
order (in velocity) emission of electromagnetic energy
in terms of the charge dipole
$$
\begin{eqnarray}
\dot E &=& -\frac{2 }{3}\langle \ddot Q^i \ddot Q_i
\rangle, \\
Q^{i} &=& \int \rm d^3 x\, j^t x^i ,
\end{eqnarray}
$$
and \(j^t=\sum_i q_i\delta (\vec x - \vec x_i)\) is the
charge density. We can do similarly with angular
momentum to find a coupled, first order differential
equation system for \(a,e\) in terms of \(E,L\), see the
thesis
for more details. The resultant equation system, not thinking
about gravitational wave emission for the moment, is
$$
\begin{eqnarray}
- \dot E &=&
\frac{\tilde G M \mu}{2 a^2}\dot a = \frac{\left(\tilde G M \mu\right)^2 \left( \Delta\sigma\right)^2}{3 a^4 (1-e^2)^{5/2}}(2+e^2),\\
-\dot J &=& \sqrt{\frac{\tilde G M \mu^2}{4 a(1-e^2)}}\left(
\dot a (1-e^2) - 2 a e \dot e\right)
= \frac{2 \mu^2 \left(\tilde G M \right)^{3/2}\left(\Delta\sigma\right)^2 }{3 a^{5/2}(1-e^2)},
\end{eqnarray}
$$ Which solves to a type of evolution for the orbit shown
below.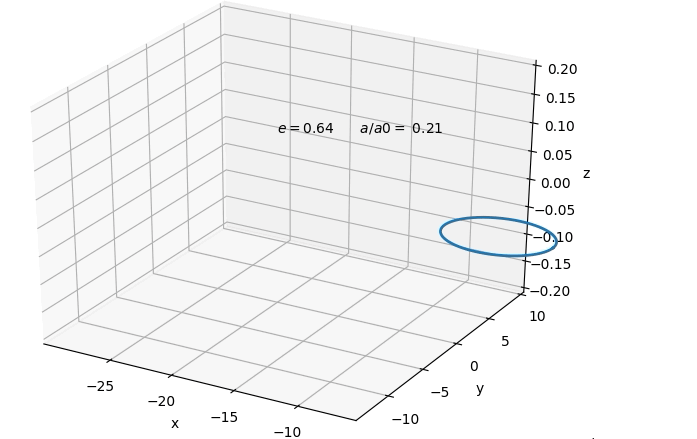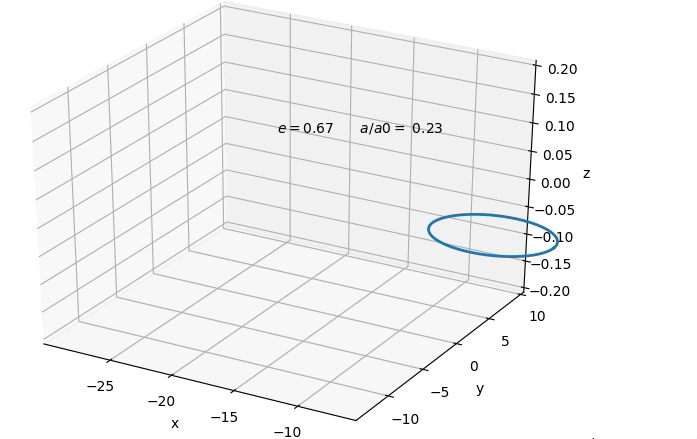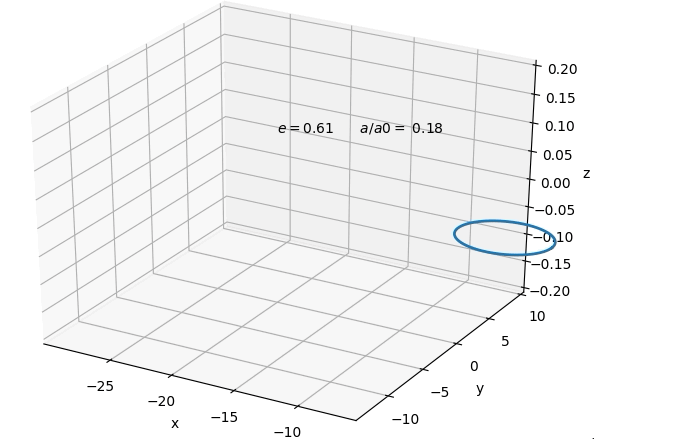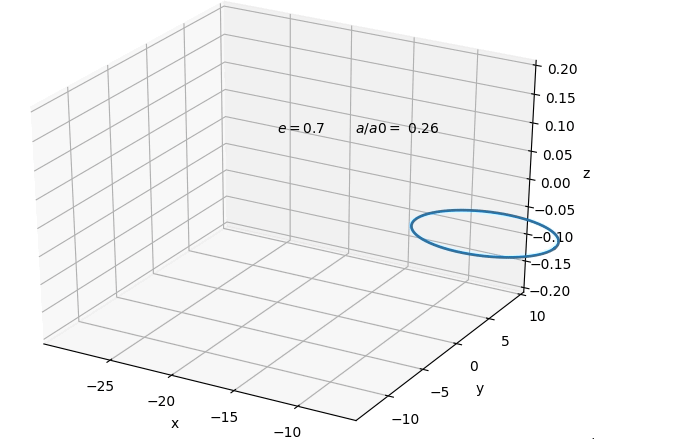 
A nice result is that orbits at originally sufficiently
large enough separation, tend to circularise by the time
its gravitational wave emission would enter into
detector sensitivity. This would allow us to at first
only consider circular orbits in the remaining. However,
we find that although the orbit circularises in both
cases, in general it is a smaller degree of
circularisation in the case of dominating
electromagnetic emission, than for gravitational
emission. Below one can see the absolute of the change
in eccentricity in response to a small fractional change
in semi-major axis for the binary system. In both cases
the eccentricity is decreasing with smaller separation. 
Matched filter and parameter bias
Equipped with the quasi-static orbital evolution, we can find
the gravitational emission in terms of the orbital parameters,
and therefore the waveform during the inspiral, to lowest order.
The waveform depends on parameters such as distance to the source,
orientation of the detector, orientation of the binary, et cetera.
We are interested in the projection effects on the black hole
parameters, so we consider the case of pure plus polarisation
radiation, and the relevant part of the waveform is
$$
h = \omega^{2/3}\sin\Psi,
$$
where \(\omega\) is the angular frequency of the binary.
For the full derivation, see the thesis. Since the detectors are most sensitive to the phase
of the signal, we can get a sense of the expected
parameter bias by considering it in isolation. It is
given
$$
\frac{5 \Psi}{16 \tau_0}\left(\frac{8\tau_0}{3 A}\right)^{3/8} \equiv \tilde \Psi =
1 - u^{5/8} -
q\left(1- u^{7/8}\right),
$$ where \(u=\tau/\tau_0\) is the time-parameter and
\(\tau\) is the time until coalescence, \(\tau_0\) being
the initial time until coalsescense. We have defined \(
A = \frac{5}{96\mathcal{M}_*^{5/3}}\),
where \(\mathcal M_*\) is the 'chirp mass'. Below, we
show the projection effect we find in the chirp mass
along the right hand y-axis. The orange line indicates
the expected result from doing a least squares phase
matching between charged and neutral waveform templates.
The blue crosses are the results after doing a matched
filtering matching, with simple LIGO/Virgo noise
modelling. On the left hand side y-axis, we see the loss
of signal incurred by the projection. The x-axis is
\(\Delta \sigma=\sigma_2-\sigma_1\), or the
charge-over-mass-difference. 
Conclusion
We found the projection effect on the parameter
estimation and the signal to be at most \(\sim 5\%\) in
the worst case considered here. This analysis serves as
a proof of concept and initial consideration, but a more
thorough analysis would take into account the ringdown
and the merger phases of the merger as well, the merger
being where the majority of the signal is found.
Furthermore, the inspiral should be performed at higher
order, and the effects on the full parameter space
should be taken into account, including intrinsic and
extrinsic binary parameters. A more general takeaway may
be that should be careful to interpret the observed
mergers as definite exclusions of more exotic sources,
seen as we might simply not have modelled them well
enough to be sensitive to them, or they may indeed be
degenerate with standard GR black holes and cause
parameter biases. However, the graviational detector
network is also applying model-independent searches,
looking for more general waveforms without matched
filtering. Employment of such search strategies,
although less sensitive, will help to overcome
difficulties like the ones presented here.